Basic Math
Addends are the numbers that are being added. The result of the addition is called the sum. Addition of whole numbers requires the understanding of the properties (or special rules) of addition. Let's take a closer look at these properties.
Commutative Property of Addition:
For any two whole numbers a and b, . In other words, the order in which the numbers are added does not matter.
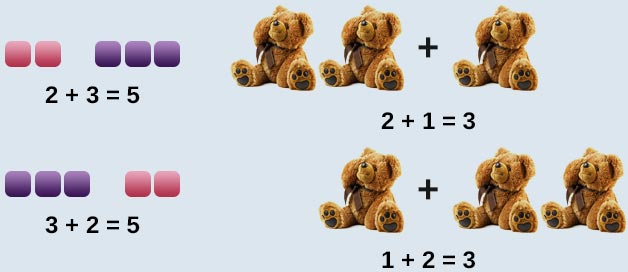
Associative property of Addition
For any whole numbers a, b and c. To add three numbers such as , we can add only two at a time, then add the third.
4 + 6 + 3
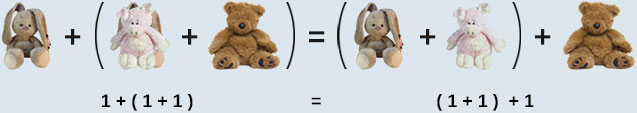

Look at
You could add these numbers in whichever order is easiest for you. All of these combinations will result in a sum of 16.
Additive Identity Property
For any whole number a,

Examples:
15 + 0 = 15
49 + 0 = 49
198 + 0 = 198
In other words, adding 0 to any number is equal to the number you started with.
Examples of all three properties:
Knowing how to apply these properties to whole numbers is an important skill needed to add. Let's see if you are getting the idea. Below are few practice problems for you to try.
Instructions: Name the addition property being illustrated.




